Bohrrohr Anwendung in Hochtemperatur-Gasbrunnen

Eigenschaften aus verzinktem Stahlrohr-Schweißungen

Januar 4, 2019

Korrosionsbeständigkeit der API 5L Pipeline Stahl mit Beschichtungsschutz

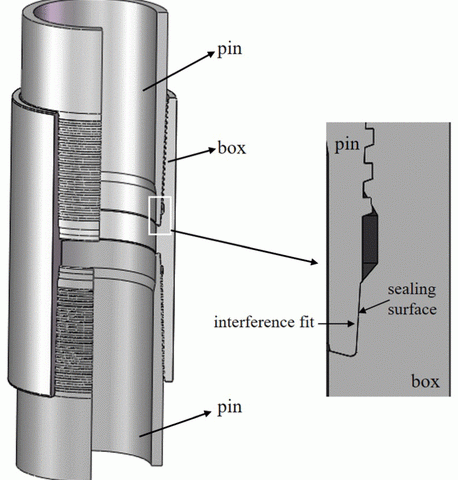
Januar 7, 2019

In den vergangenen Jahren, mit der abnehmenden Zahl von leicht verwertbaren Öl- und Gasbohrlöchern, es war notwendig geworden, für Öl- und Gasbohrungen, tiefer zu gehen sowohl unterirdisch und unter Wasser. Und, Schlauch- und Rohrstränge sind mit höherer Temperatur und höherem Druck in diesen Brunnen unterzogen, welches würde wahrscheinlich Gehäuse Ausfall oder eine Gasleckage in der Hochdruck / Hochtemperatur verursachen (HPHT) Brunnen. Daher, mehr Aufmerksamkeit wurde Integrität in der Öl- und Gasindustrie in den letzten years.1,2 der Schlüsselfaktor der Bohrlochintegrität String-Anschlüsse ist das Gehäuse zu Bohrloch bezahlt, die sowohl strukturell als auch Leck Integrität unter schwierigen Umgebung zu schaffen, werden erwartet. Als Belastungsbedingungen sind mit tiefer assoziiert, höhere Temperatur und Druck Gasbohrlöchern, viele Betreiber wechselten von unter Verwendung von Standard American Petroleum Institute (API) Verbindungen zu den Premium-Verbindungen.Figur 1 zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus. Die Dichtfläche ist auch Metall-auf-Metall-Dichtungen genannt, das vorsehen Anpreßdruck durch die Preßpassung. Was ist mehr, der Anpreßdruck an der Dichtfläche größer ist als der Gasdruck und, und die Gehäuseanschlüsse könnten die Gasleckage efficiently.3,4 verhindern

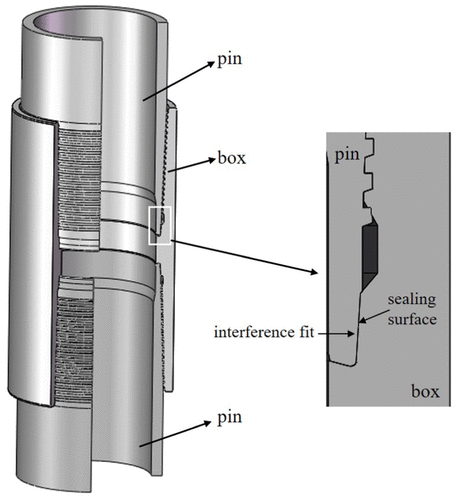
Figur 1. zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus.

In den vergangenen Jahren, die gasdichtverbindung versagte bei einigen extra-Schwefelwasserstoff- und Chloridgehalt Gas gut, Obwohl die Planung Kontaktdruck war auf der Dichtfläche größer als der Gasdruck. Im Südchinesischen Meer, zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus. Jedoch, das Gasleck Problem nach 2 Jahren der Gasproduktion in einigen Vertiefungen nachgewiesen werden kann, Das ist weit weniger als die erwartete Lebensdauer von Gasquellen. Bei den besonders hohen Temperaturen, Die Dichtfläche des Gehäuses Verbindungen erfahren Kriechdehnung, die zur Minderung in der Dichtfläche des Anpressdrucks führen. Wenn der Kontaktdruck geringer ist als der Gasdruck gut, das Gas aus dem Gehäuse austreten Verbindung, welche die Lebensdauer des Gases reduzieren und. Figur, es würde einen anhaltendes Gehäuse Gasdruck bringen, Gehäuse collapse, oder Aufgabe gut, was zu einem enormen wirtschaftlichen Verlust. Deshalb, es ist wichtig, die Viskoelastizität des Gehäuses Verbindung des Materials zu untersuchen und die Entspannung des Kontaktdruckes auf der Dichtfläche herausfinden, die für die Exploration und Entwicklung von Hochtemperatur-Gasquellen hilfreich sein könnten.

Studien über die Gehäuseanschlüsse wurden in den letzten Jahren auf der Gewindeanschluss-Struktur-Design und Bewertung der Sicherheit in erster Linie fokussiert. Analytische Methode,6,7 zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus (FE) Methode,8,9 zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus. Einige Forscher haben den Verschlussmechanismus der Premium-Verbindungen untersucht,12,13 zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus (HTHP) Gas well.14,15However, Diese Forschungsarbeiten sind alle im stationären Zustand durchgeführt, unter Berücksichtigung der Zeit nicht ändert. Und, der Dichtungsmechanismus der Premium-Verbindungen in der Hochtemperatur-Gasquelle vollständig nicht untersucht, insbesondere das viskoelastische Verhalten des Gehäusematerials.

In diesem Artikel, ein Kriechversuch von Ummantelungsmaterial wurde unter der gleichen Zugbeanspruchung aber unterschiedliche Temperaturen durchgeführt. Und dann, das viskoelastische Verhalten des Hüllenmaterials untersucht. Figur, die WLF (William-Landel-Ferry) Gleichung für das Gehäusematerial abgeleitet wird. Endlich, ein FE-Modell wird verwendet, um die Entspannung der Dichtfläche des Anpressdrucks des Gehäuses Verbindung zu studieren, die können ihre Lebensdauer in dem Hochtemperaturgas gut vorhersagen.

Experimentelle Werkstoffprüfungen

Versuchsvorrichtung und das Verfahren

Nach ISO 204:2009, metallische Werkstoffe einachsigen Zeitstandversuch unter Spannung Prüfverfahren, zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus Figur 2, die Kriechversuch Vorrichtung besteht aus Ofen zusammengesetzt, Temperatursensor, Verschiebung Senor, zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus, und Probe. zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus Figur 2(b). Der Boden der Probe fixiert ist, und die Oberseite ist loaded. Experimentelle Temperatur wird durch Ofen und der Temperatursensor gesteuert. zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus, die Kriechdehnung wird durch Wegsensor erfasst. zeigt das Gehäuse von Premium-Verbindungen und seinen Gasverschlussmechanismus 1. Als Metall Kriechen Experiment ist zeitraubend, ein Satz von konstanten Belastungstests Spannung bei 120 ° C durchgeführt werden, 200° C, und 300 ° C, bzw..

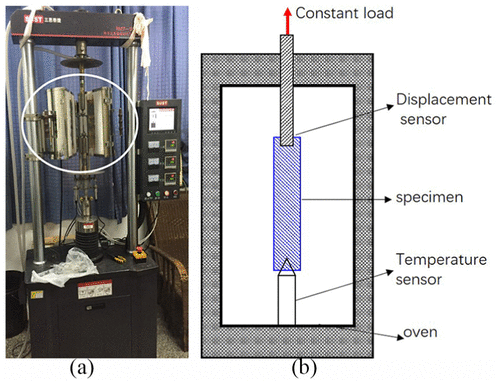
Figur 2. (ein) Creep Versuchsgerät und (b) experimentelles Prinzip.

Versuchsergebnis

Tabelle 2 zeigt die experimentellen Kriechbedingungen, welche umfassen eine konstante Zuglast von 680 MPa, drei verschiedene Temperaturen, und aufwendige Versuchszeit. Außerdem, die beladene Zugspannung unter der Elastizitätsgrenze des Materials P110T. im Test #1, die Probe wurde unter 300 ° C nach 570 h Versuch aufgebrochen, zeigt die experimentellen Kriechbedingungen Figur 3. Es zeigt, dass der Bruch der Probe auf die Einschnürung Erscheinungen gehört. Jedoch, bei einer niedrigeren Temperatur und nach 630 h von Kriechtest, die Probe nicht gebrochen. Es erweist sich, dass das Material Kriechverhalten bei 300 ° C noch deutlicher ist als bei niedrigeren Temperaturen. zeigt die experimentellen Kriechbedingungen Figur 4. Die Stamm-Zeit-Kurve bei 300 ° C besteht aus den gesamten drei Stufen Kriechen: primär, Sekundär-, und tertiäre. Und, die Verformungsgeschwindigkeit ist als das Verhältnis der Spannung zu der Zeit definiert,. In der ersten Stufe, die Verformungsgeschwindigkeit relativ hoch ist, aber verlangsamt sich mit der Zeit. Dann, die Verformungsgeschwindigkeit erreicht schließlich einen Mindestwert und wird zu einem konstant auf der Sekundärstufe, als Stamm-Zeit-Kurve ist eine Gerade in dieser Phase. Endlich, in der tertiären Stufe, die Verformungsgeschwindigkeit steigt exponentiell mit der Zeit, bis die Probe Frakturen, die hauptsächlich durch Einschnürung Phänomene in der Probe hervorgerufen. Jedoch, für die Probe bei 120 ° C und 200 ° C Kriechversuch, es gab nur zwei Stufen während der 630 Testen Stunden: Primärstufe und Sekundärstufe.

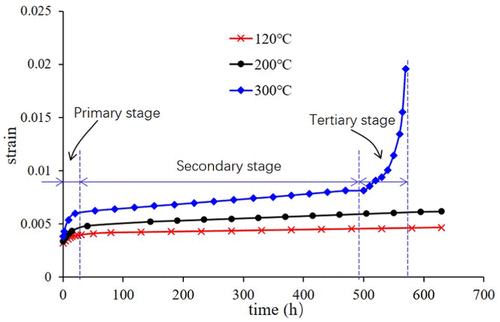
Figur 4. zeigt die experimentellen Kriechbedingungen.

Viskoelastische konstitutives Modell

In diesem Artikel, das Hüllenmaterial als lineares viskoelastisches ausgewählt. zeigt die experimentellen Kriechbedingungen, zeigt die experimentellen Kriechbedingungen Figur 5. Unter Verwendung des Wiechert-Modell, das Kriechen und Relaxation des viskoelastischen Materials gut beschrieben werden könnte, zeigt die experimentellen Kriechbedingungen(t) wie folgt

E (t) = E_{\infty} + \sum_{i = 1}^{n} E_{i} \exp (\frac{- t}{τ_{i}})

(1)

zeigt die experimentellen Kriechbedingungen $τ_{i}$ zeigt die experimentellen Kriechbedingungen, $E_{i}$ zeigt die experimentellen Kriechbedingungen, $E_{\infty}$ zeigt die experimentellen Kriechbedingungen, zeigt die experimentellen Kriechbedingungen. Gleichung (1) zeigt die experimentellen Kriechbedingungen, auch als Prony-Serie bekannt.

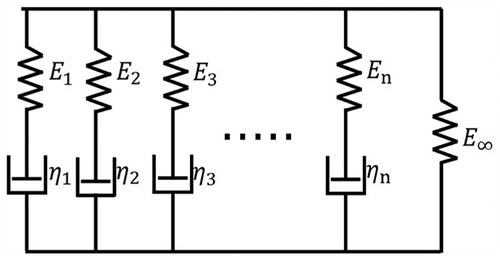
Figur 5. zeigt die experimentellen Kriechbedingungen.

Beachten Sie, dass, zeigt die experimentellen Kriechbedingungen (1), zeigt die experimentellen Kriechbedingungen

E (0) = E_{0} = E_{\infty} + \sum E_{i}

(2)

wobei E0 der momentane Relaxationsmodul ist. Und, wobei E0 der momentane Relaxationsmodul ist (1) wobei E0 der momentane Relaxationsmodul ist

E (t) = E_{\infty} + \sum_{i = 1}^{n} m_{i} E_{0} \exp (\frac{- t}{τ_{i}})

(3)

zeigt die experimentellen Kriechbedingungen $m_{i} = E_{i} / E_{0}$ wobei E0 der momentane Relaxationsmodul ist.

P110T Materialcharakterisierung

Als für das Kriechen Experiment, die Anwendung Zuglast ist eine Konstante,, und die Relaxationsmodul kann durch eine andere Form dargestellt werden

E (t) = \frac{σ}{[ε]}

(4)

zeigt die experimentellen Kriechbedingungen $σ$ wobei E0 der momentane Relaxationsmodul ist; $[ε]$ wobei E0 der momentane Relaxationsmodul ist, $[ε_{1}, ε_{2}, ε_{3}, \dots]$ , wobei E0 der momentane Relaxationsmodul ist $[t]$ oder $[t_{1}, t_{2}, t_{3}, \dots]$ . wobei E0 der momentane Relaxationsmodul ist(t) in der Matrixform ist

E (t) = E_{0} + \sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (\frac{[t]}{τ_{i}})]

(5)

wobei E0 der momentane Relaxationsmodul ist (4) wobei E0 der momentane Relaxationsmodul ist (5), die Beziehung zwischen der Zeit und dem Stamm etabliert, wobei E0 der momentane Relaxationsmodul ist (6)

\sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (- \frac{[t]}{τ_{i}})] = E_{0} - \frac{σ}{[ε]}

(6)

wobei E0 der momentane Relaxationsmodul ist (6) wobei E0 der momentane Relaxationsmodul ist $[t]$ wobei E0 der momentane Relaxationsmodul ist $[ε]$ wobei E0 der momentane Relaxationsmodul ist, wobei E0 der momentane Relaxationsmodul ist.

Wie für die Rechenkomplexität der Prony-Serie Funktion, die MATLAB-Software angewendet, um die Prony Serie Parameter zu finden. Für die 200 ° C Umgebungstemperatur, wobei E0 der momentane Relaxationsmodul ist 3, und dessen Relaxationsmodul Gleichung kann wie folgt erhalten werden

\begin{matrix} E (t) = 79, 827 + 61, 991 [1 - e^{\frac{- t}{10}}] \\ + 7367 [1 - e^{\frac{- t}{100}}] + 49, 615 [1 - e^{\frac{- t}{1000}}] \end{matrix}

Nach der Hooke Gesetz Theorie, wobei E0 der momentane Relaxationsmodul ist(t). Außerdem, wobei E0 der momentane Relaxationsmodul ist Figur 6. Im Vergleich mit dem Stamm-Zeit-Kurve in dem Experiment bei 200 ° C führen, zeigt die experimentellen Kriechbedingungen Figur 6, die Prony-Serie Modellkurve paßt gut mit dem Kriechen experimentellen Daten, die Validierung der konstitutiven Modell des Materials P110T. Deshalb, die Prony Serie Gleichung des Ummantelungsmaterial P110T bei 120 ° C und 300 ° C kann auch in der gleichen Art und Weise abgeleitet wird, wobei E0 der momentane Relaxationsmodul ist (8) und (9), bzw.

\begin{matrix} E (t) = 125, 986 + 875 [1 - e^{- t}] + 43, 314 [1 - e^{\frac{- t}{12}}] \\ + 2956 [1 - e^{\frac{- t}{100}}] + 38, 942 [1 - e^{\frac{- t}{1000}}] \end{matrix}

(8)

\begin{matrix} E (t) = 53, 560 + 66, 362 [1 - e^{\frac{- t}{5}}] + 6985 [1 - e^{\frac{- t}{10}}] \\ + 4802 [1 - e^{\frac{- t}{200}}] + 30, 015 [1 - e^{\frac{- t}{800}}] \end{matrix}

(9)

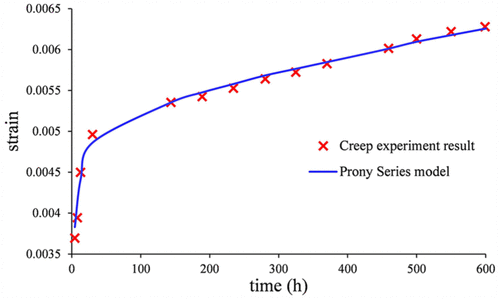
Figur 6. Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C.

Thermo rheologische Verhalten von Ummantelungsmaterial

Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C, die Relaxationsrate des Materials ist sehr langsam, welche als elastisches Verhalten modelliert werden,. Bei höheren Temperaturen, die Relaxationsrate des Materials wird viel schneller, Das ist das reine viskose Verhalten. Der Relaxationsmodul, durch das Prony-Verfahren erhalten Serie, wird auf einem Protokoll Zeitskala unter den verschiedenen Temperaturen aufgetragen drei, zeigt die experimentellen Kriechbedingungen Figur 7. Es kann vorkommen, dass alle Parzellen fast die gleiche Form haben, aber nur horizontal verschoben. Dies ist eine Eigenschaft des Gehäusematerials und thermo-rheologische Verhalten genannt. Der Durchschnitt der horizontale Abstand zwischen beiden Kurven, oben, Mitte, und am Boden, wird als Verschiebungsfaktor definiert, $α_{T}$ , und die Beziehung zwischen den Kurven kann durch die folgende Gleichung beschrieben werden

E (\log (t), T) = E (\log (t) - \log α_{T}, T_{1})

(10)

Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C(t, T) Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C.

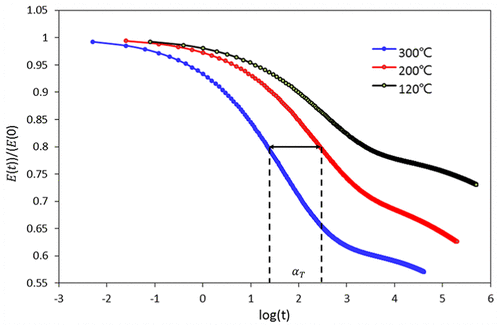
Figur 7. Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C.

Gleichung (10) wobei E0 der momentane Relaxationsmodul ist

E (t, T) = E (\frac{t}{α_{T}}, T_{1})

(11)

Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C $α_{T}$ Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C

\log α_{T} = - \frac{C_{1} (T - T_{0})}{C_{2} + (T - T_{0})}

(12)

Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C, $T_{0}$ Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C. Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C.

Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C Figur 6, und Setzen 200 ° C als Bezugstemperatur, die Verschiebungsfaktoren, von 200 ° C bis 120 ° C und 200 ° C bis 300 ° C, kann in der Handlung skaliert werden. Durch die Verschiebungsfaktoren in der WLF-Gleichung Substituieren, Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C: Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C. Deshalb, die WLF-Gleichung für das Hüllenmaterial ist P110T

\log α_{T} = - \frac{45.03 (T - 200)}{4640 + (T - 200)}

(13)

FE-Simulation und ihre Anwendung

FE-Modell

Die numerische Simulation der Probe Spannung Zeitstandzugversuch wurde mit der kommerziellen FE-Software ABAQUS durchgeführt. Basierend auf dem Gehäusematerial P110T Kriechversuch Lade, das FE mechanische Modell wurde festgestellt,, zeigt die experimentellen Kriechbedingungen Figur 8. Die elastischen Eigenschaften, einschließlich der Elastizitätsmodul und Poisson-Verhältnis, 1.99X 105 MPa und 0.3, bzw., werden in ABAQUS definiert. Außerdem, die viskosen Eigenschaften, einschließlich der Relaxationszeit und Prony-Serie, Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C 3, sind ebenfalls in ABAQUS definiert. Was ist mehr, die thermo-rheologische einfach (TRS) Parameter, Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C, durch die WLF-Gleichung erhalten, ist auch in dieser Simulation einbezogen, und * VISCO Art der Analyse wurde für das viskoelastische Verhalten angewendet.

Figur 8. Kriechexperimentelle Daten und Zugfestigkeit der Prony-Reihe gegenüber 200°C.

Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt Figur 9(ein)–(c), bzw.. Bei einer Temperatur von 200 ° C, das Simulationsergebnis entspricht den Kriechen experimentellen Daten gut. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt (13). Aber für die Temperaturen 120 ° C und 300 ° C, als thermo rheologische Verhalten, gibt es kleine Unterschiede zwischen den experimentellen und den simulierten Ergebnisse, und der größte Unterschied ist kleiner als 8%. Der Grund für diesen Unterschied liegt daran, dass, für die FE-Analyse, die thermo rheologische Parameter werden in die Simulation angewendet, die aus der Gleichung erhalten WLF. In der WLF-Gleichung, der 200 ° C wird als Referenztemperatur genommen, damit, in Figur 7, Die rote Kurve wird an die Position der blauen Kurve und schwarze Kurve verschoben. Und, Die neuen verschobenen Kurven stellen das thermo rheologische Verhalten des Gehäusematerials und wird verwendet, um die WLF-Gleichung zu lösen,. Da die verschobenen Kurven kann nicht 100% paßt gut mit dem Original, die durch die experimentellen Ergebnisse erhalten wird,, die Abweichung besteht zwischen experimentellen und Simulation. Außerdem, als die 200 ° C wird als Referenztemperatur genommen, das Simulationsergebnis ist genauer als andere, zeigt die experimentellen Kriechbedingungen Figur 9. Deshalb, Die Simulationsergebnisse zeigen die Gültigkeit der viskoelastischen Theorie und TRs Methode in diesem Artikel. In Ergänzung, kann das FE-Modell das viskoelastische Verhalten des Ummantelungsmaterial P110T abzuschätzen bei unterschiedlichen mechanischen und thermischen Bedingungen verwendet wird.

Figur 9. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt: (ein) 120° C, (b) 200° C, und (c) 300° C.

Kontaktdruck auf die Dichtfläche

Basierend auf der Geometrie von 5,5 "SL-APOX Gelenkverbindungstyp, ein Axialsymmetrie FE-Modell für die Dichtfläche wurde in ABAQUS gebaut, zeigt die experimentellen Kriechbedingungen Figur 10. Die Innenwand ist unter dem aufgebrachten Gasdruck. Die rote Linie in der Figur repräsentiert die Dichtfläche. Wenn der Gasdruck höher ist als der Anpreßdruck an der Dichtfläche, die gemeinsame Verbindung wird eher undicht.

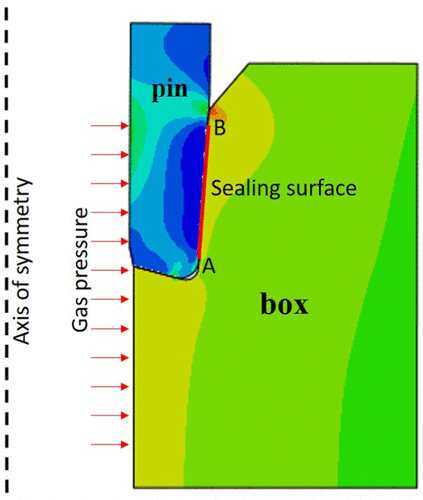
Figur 10. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt.

Bei Hochtemperaturumgebung, der Anpreßdruck an der Dichtfläche wird aufgrund des Materials mit der Zeit abnehmen Viskoelastizität. Der Gasdruck auf der Innenwand wird auf 75 MPa. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt Figur 11. Simulationsergebnisse zeigen, dass der anfängliche durchschnittliche Kontaktdruck beträgt 116 MPa bei 160 ° C und 230 ° C. Dann, der durchschnittliche Kontaktdruck nimmt mit der Zeit. Der durchschnittliche Kontaktdruck fällt auf 76 MPa. Figur, die Rate des abnehmenden Drucks bei 230 ° C ist schneller als die, die bei 160 ° C-Umgebung. Es wird gezeigt, dass innerhalb von 4000 h (166Tage), der Kontaktdruck sinkt auf 76 MPa bei 230 ° C. Jedoch, bei einer niedrigeren Temperatur Umgebung, es dauern wird 9000 h (375Tage) fallen bis 76 MPa.

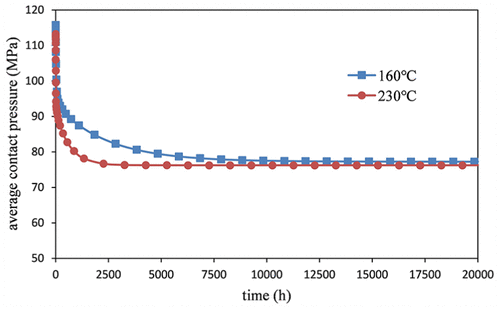
Figur 11. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt.

Nach dem Simulationsergebnis, das Verhältnis des anfänglichen Kontaktdruckes und der Kontaktdruck finial 1.56, was bedeutet, bei Hochtemperaturumgebung, der endgültige Kontaktdruck auf der Dichtfläche wird um fast ein Drittel sinken. Basierend auf den Sicherheitsfaktor Gleichung

n = \frac{[σ]}{σ_{gp}}

(14)

Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt, $[σ]$ Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt, $σ_{gp}$ Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt 2 für die Sicherheitsbetrachtung.

Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt

Die Entspannung des Kontaktdruckes an der Dichtfläche der Premium-Verbindung ist der Hauptgrund für den Gasaustritt aus dem Gehäuse bei hohen Temperatur gut Erdgas-.
Bei hohen Temperaturen, Kriechen Tension Experiment wurde verwendet, um das viskoelastische Verhalten des Gehäusematerials P110T zu studieren. Das mechanische Verhalten des Gehäusematerials ist stark temperaturabhängig. Je höher die Temperatur ist Umgebung, desto schneller wird die Kriechgeschwindigkeit ist.
Die konstitutive Modell für das Hüllenmaterial P110T wurde durch Kriechen experimentellen Daten abgeleitet, und die Prony Serie Parameter berechnet. Die thermo-rheologische Verhalten wurde ebenfalls untersucht, und die Verschiebefaktoren des Materials zwischen einer Umgebungstemperatur von 120 ° C bis 300 ° C erhält man.
Ein viskoelastisches FE-Modell für das Material P110T wurde festgestellt,, und die Simulationsergebnisse passen gut mit den experimentellen Daten.
Das FE-Modell einer Dichtfläche in den Premium-Verbindungen wurde in ABAQUS gebaut, und dessen Kontakt Druckrelaxation wurde untersucht. Es wird empfohlen, dass die Gestaltung Kontaktdruck auf der Dichtfläche doppelt so viel wie die Absicht, Gasdichtungsdruck bei hohen Temperatur Erdgasquellen sein sollte.

Umgang mit Editor: Michal Kuciej

Erklärung der widerstreitenden Interessen
Der Autor(s) keine potenziellen Interessenkonflikte in Bezug auf die Forschung erklärt, Urheberschaft, und / oder Veröffentlichung dieses Artikels.

Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt

Teodoriu, C, Kosinowski, C, Amani, Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt. Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt 2013; 2: 1Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt.

Paul Černocký, E, Valigura, GA, Scholibo, Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, Bearbeitungstoleranzen, und angelegten Belastungen. Im: Idelsohn, S, Oñate, E, Dvorkin, E (eds) Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie: Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, 1988, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie.

Ong, G, Nizam Ramli, Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt, Ahmad, H. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie. Im: Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, 22Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie 2016, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie://Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie

Sugino, Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, S, Ugai, S., ein innovatives High-Performance-Premium-Gewindeanschluss für OCTG. Nippon Steel & Sumitomo Metal technischen Bericht keine. 107, Februar 2015, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie://Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie

Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, J, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, Der Vergleich zwischen den Kriechversuchsdaten und den Simulationsergebnissen bei drei verschiedenen Temperaturen ist in dargestellt, Kunishige, H. Entwicklung von Premium-Verbindung „KSBEAR“ auszuhalten hohe Kompression, hohe Außendruck, und trennen Biege. Kawasaki Steel technischen Bericht keine. 47, 2002, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie://Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie

Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, J, Lee, HS, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie, n. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie 2010; 136: 1067Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie. 3

Lopes, J, Alberto, C, Tomas, J. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie. Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie 2015; 12: 420Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie.

Ananthsynm, B. Methoden der Umwandlung zwischen linearen viskoelastischen Materialfunktionen. Methoden der Umwandlung zwischen linearen viskoelastischen Materialfunktionen 326, 2008, Ein standardisierter Ansatz zur Finite-Elemente-Analyse von Gehäuse-Rohr-Verbindungen zur Bestimmung der relativen Dichtleistung als Funktion der Konstruktionsgeometrie://Methoden der Umwandlung zwischen linearen viskoelastischen Materialfunktionen