Yüksek sıcaklıklı gaz kuyularında muhafaza borusu uygulaması

Galvaniz boru kaynaklarının özellikleri

Ocak 4, 2019

Kaplama Koruma API 5L Boru Hattı Çeliğin Korozyon Direnci

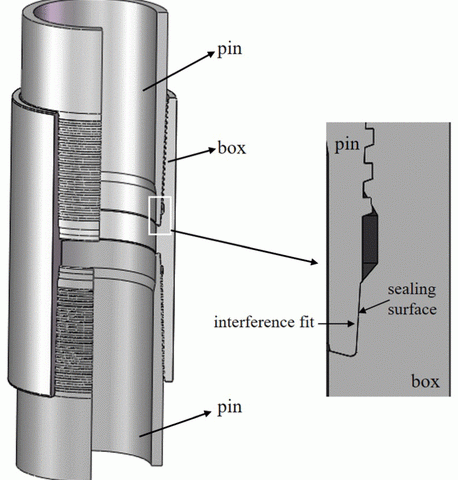
Ocak 7, 2019

Son yıllarda, kolaylıkla yararlanılabilir petrol ve gaz kuyularının azalan sayıda, petrol ve gaz kuyuları hem yeraltı ve sualtı üzerinde derin gitmek için gerekli hale gelmiştir. Ve, boru ve kılıf şeritler bu kuyuların daha yüksek sıcaklık ve yüksek basınca maruz, Muhtemelen yüksek basınç / yüksek sıcaklık muhafaza yetmezliği ya da gaz sızmasını neden olacak (HPHT) kuyular. Bu nedenle, daha fazla dikkat dize bağlantılarını Çakma olan son years.1,2 içinde kuyu bütünlüğünün önemli faktör petrol ve gaz sektöründe bütünlüğünü kuyunun açılması için ödendi, Şiddetli ortamda hem yapısal hem de sızıntı bütünlük sağlamak için beklendiği. yükleme koşulları daha derin ilişkili olarak, Daha yüksek sıcaklık ve basınç gaz kuyusu, birçok operatör standart American Petroleum Institute kullanarak açık (API) prim bağlantıları bağlantıları.şekil 1 Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir. sızdırmazlık yüzeyi de bir metal-metal contalar olarak adlandırılır, sıkı geçme yoluyla temas basıncı sağlayan. Dahası, sızdırmazlık yüzeyi ile bir temas basıncı gaz kuyusu basıncından daha yüksektir, ve gövde bağlantıları gaz kaçağı efficiently.3,4 önlenebilmektedir

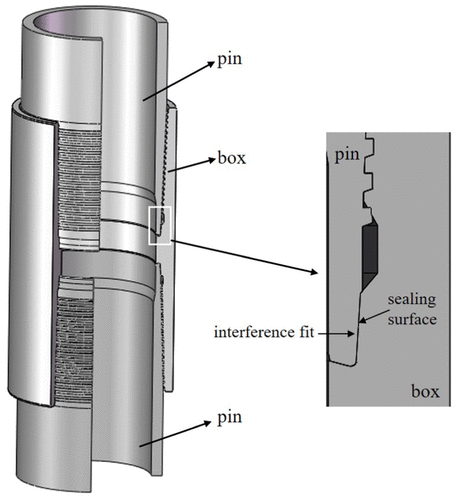
şekil 1. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir.

Son yıllarda, bazı ekstra durumlarda gaz sızdırmazlık bağlantısı başarısız oldu-Yüksek sıcaklık gaz kuyusu, Sızdırmazlık yüzeyi üzerinde tasarımı temas basıncı gaz basıncından daha yüksek olmasına rağmen. Güney Çin'de Deniz, Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir. ancak, Gaz kaçağı problemi bazı kuyularda gaz üretiminin 2 yıl sonra saptanabilir, hangi gaz kuyuları beklenen ömrü çok daha azdır. Ekstra yüksek sıcaklıklarda, mahfaza bağlantılarının sızdırmazlık yüzeyi sünme suşu karşılaşacaklardır, hangi sızdırmazlık Yüzeyin temas basıncındaki azalmaya yol açacaktır. Temas basıncı gaz kuyusu basıncından daha düşük olduğunda, Gaz gövde bağlantısından sızıntı, hangi iyi gaz kullanım ömrünü azaltacaktır. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir, Bu sürekli bir kılıf gaz basıncının getirecek, mahfaza çöküşü, veya iyi Vazgeçme, büyük ekonomik kayıplara neden. bu nedenle, kovan bağlantının malzemenin viskoelastikliğe çalışma ve sızdırmazlık yüzeyinde temas basıncının rahatlama öğrenmek için önemlidir, Yüksek sıcaklıklı gaz kuyularının araştırma ve geliştirme için yararlı olabilir ki.

kasa bağlantılarında Araştırma çalışmaları ağırlıklı olarak geçtiğimiz yıllarda iplik bağlantısı yapısı tasarımı ve güvenlik değerlendirmesinde üzerinde yoğunlaşmış bulunmaktadır. Analitik metod,6,7 Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir (FE) yöntemi,8,9 Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir. Bazı araştırmacılar prim bağlantılarının sızdırmazlık mekanizması araştırdık,12,13 Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir (HTHP) gaz well.14,15However, Bu araştırma çalışmaları tüm sabit halde yapılmaktadır, zaman değişiyor düşünmediğini. Ve, Yüksek sıcaklık gaz kuyusundan prim bağlantılarının sızdırmazlık mekanizması tam olarak araştırılmamıştır, mahfaza malzemesinin özellikle viskoelastik davranış.

Bu makalede, mahfaza malzemesinin bir sürünme deneyi olarak aynı gerilme, gerilme, ancak farklı sıcaklıklarda gerçekleştirilmiştir. Ve sonra, mahfaza maddesi viskoelastik davranış incelenmiştir. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir, WLF (William-Landel-Ferry) gövde malzemesi için denklem türetilmiştir. En sonunda, FE modeli mahfaza bağlantının sızdırmaz yüzeyin temas basıncının gevşeme incelemek için kullanılır, hangi yüksek sıcaklık gaz kuyuda ömrünü tahmin edebilirsiniz.

Deneysel malzeme testleri

Deneysel düzenek ve işlem

ISO göre 204:2009, Testin gerilim yöntemde metalik malzemelerin tek eksenli sünme testi, Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir şekil 2, sürünme deneyi cihazı fırın oluşmaktadır, Sıcaklık sensörü, deplasman senor, Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir, ve numune. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir şekil 2(b). numunenin alt sabittir, ve en yüklendiğinde. Deneysel sıcaklık fırın ve sıcaklık sensörü ile kontrol edilir. o esnada, Sürünme suşu yer değiştirme sensörü tarafından kaydedilir. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir 1. Metal sürünme deneyi olarak zaman alıcıdır, Sabit gerilim yükü bir küme deney 120 ° C sıcaklıkta gerçekleştirilmektedir, 200° C, ve 300 ° C, sırasıyla.

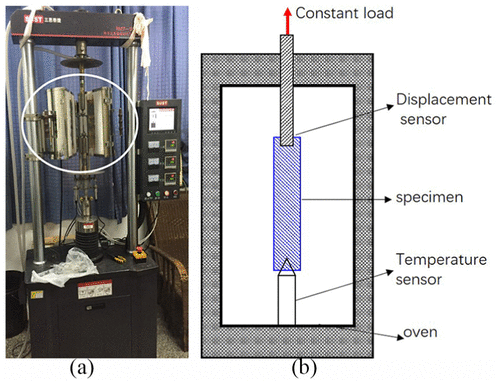
şekil 2. (bir) Sürünme deney cihazı ve (b) deneysel ilkesi.

Deneysel sonuç

Tablo 2 sürünme deney koşullarını gösterir, olan 680 MPa sabit bir gerilme yükü içerir, Üç farklı sıcaklıklar, ve deneysel zaman alıcı. Ayrıca, yüklü çekme gerilimi P110T materyalin elastik sınırının altındadır. testte #1, Numune, 300 ° C'nin altında 570 saat deneyden sonra kırılmış, sürünme deney koşullarını gösterir şekil 3. Bu numunenin kırılma Daraltma fenomenlerin ait olduğunu gösterir. ancak, daha düşük bir sıcaklıkta ve sürünme test 630 saat sonra, Numune kırığı yoktu. Bu, 300 ° C'de malzeme sürünme daha düşük sıcaklıklarda daha bariz olduğunu kanıtlar. sürünme deney koşullarını gösterir şekil 4. 300 ° C 'de baskı-zaman eğrisi bütün üç sürünme aşamadan oluşmaktadır: birincil, ikincil, ve üçüncül. Ve, Gerilme hızı zaman suşun oranı olarak tanımlanır. ilk aşamada, Gerilme hızı nispeten yüksektir, ancak zamanla yavaşlar. Sonra, Gerilme hızı, sonunda bir minimum değere ulaştığında ve ikinci aşamada bir sabit değer haline gelir, baskı-zaman eğrisi olarak, bu aşamada bir düz çizgidir. En sonunda, üçüncü aşamada, Gerilme hızı katlanarak numune kırılana dek zamanla artar, temel olarak örnek olarak fenomeni boyun neden olduğu. ancak, 120 ° C ile 200 ° C sürünme deneyi de numune için, Sadece iki aşamaları sırasında vardı 630 test saatleri: ilk aşama ve ikinci aşama.

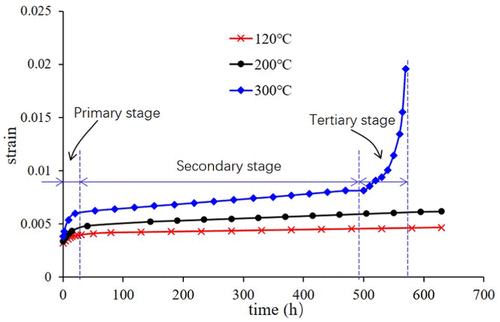
şekil 4. sürünme deney koşullarını gösterir.

Viskoelastik kurucu modeli

Bu makalede, kılıf malzemesi lineer viskoelastik olarak seçilir. sürünme deney koşullarını gösterir, sürünme deney koşullarını gösterir şekil 5. Wiechert modeli kullanarak, viskoelastik materyalin sünme ve gevşeme de tanımlanabilir, sürünme deney koşullarını gösterir(t) aşağıdaki gibi

E (t) = E_{\infty} + \sum_{i = 1}^{n} E_{i} \exp (\frac{- t}{τ_{i}})

(1)

sürünme deney koşullarını gösterir $τ_{i}$ sürünme deney koşullarını gösterir, $E_{i}$ sürünme deney koşullarını gösterir, $E_{\infty}$ sürünme deney koşullarını gösterir, sürünme deney koşullarını gösterir. Denklem (1) sürünme deney koşullarını gösterir, Ayrıca Prony dizisi olarak da bilinen.

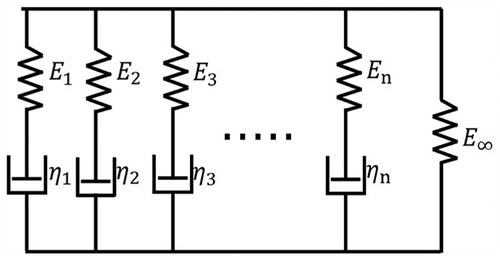
şekil 5. sürünme deney koşullarını gösterir.

Bunu not et, sürünme deney koşullarını gösterir (1), sürünme deney koşullarını gösterir

E (0) = E_{0} = E_{\infty} + \sum E_{i}

(2)

burada E0 anlık gevşeme modülüdür. Ve, burada E0 anlık gevşeme modülüdür (1) burada E0 anlık gevşeme modülüdür

E (t) = E_{\infty} + \sum_{i = 1}^{n} m_{i} E_{0} \exp (\frac{- t}{τ_{i}})

(3)

sürünme deney koşullarını gösterir $m_{i} = E_{i} / E_{0}$ burada E0 anlık gevşeme modülüdür.

P110T malzeme karakterizasyonu

sürünme deneyi için olduğu gibi, Uygulama gerilim yükü bir sabittir, ve dinlenme modülü başka bir formda ile temsil edilebilir:

E (t) = \frac{σ}{[ε]}

(4)

sürünme deney koşullarını gösterir $σ$ burada E0 anlık gevşeme modülüdür; $[ε]$ burada E0 anlık gevşeme modülüdür, $[ε_{1}, ε_{2}, ε_{3}, \dots]$ , burada E0 anlık gevşeme modülüdür $[t]$ veya $[t_{1}, t_{2}, t_{3}, \dots]$ . burada E0 anlık gevşeme modülüdür(t) matris biçimindedir

E (t) = E_{0} + \sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (\frac{[t]}{τ_{i}})]

(5)

burada E0 anlık gevşeme modülüdür (4) burada E0 anlık gevşeme modülüdür (5), Zaman ve zorlanma arasındaki ilişki kurulur, burada E0 anlık gevşeme modülüdür (6)

\sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (- \frac{[t]}{τ_{i}})] = E_{0} - \frac{σ}{[ε]}

(6)

burada E0 anlık gevşeme modülüdür (6) burada E0 anlık gevşeme modülüdür $[t]$ burada E0 anlık gevşeme modülüdür $[ε]$ burada E0 anlık gevşeme modülüdür, burada E0 anlık gevşeme modülüdür.

Prony dizi işlevinin işlem karmaşıklığına gelince, MATLAB yazılımı Prony serisi parametreyi bulmak için uygulanır. 200 ° C, çevre sıcaklığı için, burada E0 anlık gevşeme modülüdür 3, aşağıdaki gibi ve gevşeme modülü denklemi elde edilebilir

\begin{matrix} E (t) = 79, 827 + 61, 991 [1 - e^{\frac{- t}{10}}] \\ + 7367 [1 - e^{\frac{- t}{100}}] + 49, 615 [1 - e^{\frac{- t}{1000}}] \end{matrix}

Hooke kanunu teorisine göre, burada E0 anlık gevşeme modülüdür(t). Ayrıca, burada E0 anlık gevşeme modülüdür şekil 6. Deneyde baskı-zaman eğrisi ile karşılaştırıldığında, 200 ° C 'de neden, sürünme deney koşullarını gösterir şekil 6, Prony serisi modeli eğrisi sürünme deneysel verilerle iyi uyum, ki P110T malzemesinin kurucu modeli doğrulamak. bu nedenle, 120 ° C ve 300 ° C 'de muhafaza malzemesi P110T arasında Prony dizi denklem de aynı şekilde elde edilebilir, burada E0 anlık gevşeme modülüdür (8) ve (9), sırasıyla

\begin{matrix} E (t) = 125, 986 + 875 [1 - e^{- t}] + 43, 314 [1 - e^{\frac{- t}{12}}] \\ + 2956 [1 - e^{\frac{- t}{100}}] + 38, 942 [1 - e^{\frac{- t}{1000}}] \end{matrix}

(8)

\begin{matrix} E (t) = 53, 560 + 66, 362 [1 - e^{\frac{- t}{5}}] + 6985 [1 - e^{\frac{- t}{10}}] \\ + 4802 [1 - e^{\frac{- t}{200}}] + 30, 015 [1 - e^{\frac{- t}{800}}] \end{matrix}

(9)

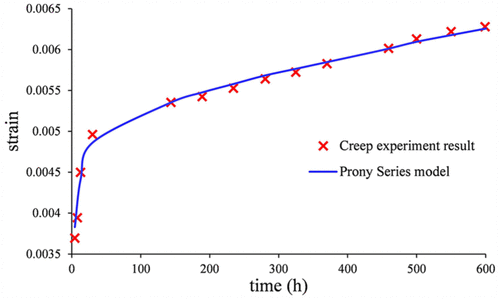
şekil 6. 200°C'de sürünme deney verileri ve Prony serisi çekme.

mahfaza maddesi termo reolojik davranışı

200°C'de sürünme deney verileri ve Prony serisi çekme, malzemenin gevşeme oranı çok yavaş, esnek bir davranış modellenebilecegi. Daha yüksek sıcaklıklarda, malzemenin gevşeme oranı çok daha hızlı olur, bu, saf viskoz davranış. gevşeme modülü, Prony dizi yöntem ile elde edilen, Üç farklı sıcaklıklarda bir günlük bir zaman ölçeğinde çizilir, sürünme deney koşullarını gösterir şekil 7. Tüm araziler hemen hemen aynı şekle sahip ama sadece yatay olarak kaydırılır olduğu bulunabilir. Bu kaplama malzemesinin bir özelliğidir ve termo-reolojik davranış denir. iki eğri arasındaki yatay uzaklık ortalama, zirvede, Orta, ve alt, aT kaydırma faktörü olarak tanımlanmaktadır, $α_{T}$ , ve eğriler arasındaki ilişki aşağıdaki denklem ile tanımlanabilir

E (\log (t), T) = E (\log (t) - \log α_{T}, T_{1})

(10)

200°C'de sürünme deney verileri ve Prony serisi çekme(t, T) 200°C'de sürünme deney verileri ve Prony serisi çekme.

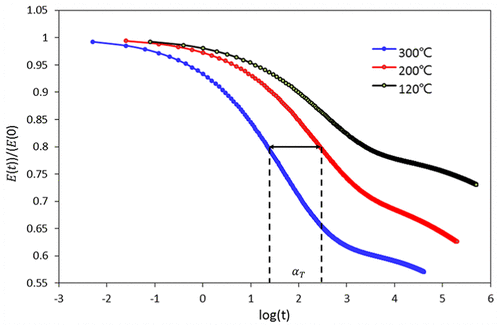
şekil 7. 200°C'de sürünme deney verileri ve Prony serisi çekme.

Denklem (10) burada E0 anlık gevşeme modülüdür

E (t, T) = E (\frac{t}{α_{T}}, T_{1})

(11)

200°C'de sürünme deney verileri ve Prony serisi çekme $α_{T}$ 200°C'de sürünme deney verileri ve Prony serisi çekme

\log α_{T} = - \frac{C_{1} (T - T_{0})}{C_{2} + (T - T_{0})}

(12)

200°C'de sürünme deney verileri ve Prony serisi çekme, $T_{0}$ 200°C'de sürünme deney verileri ve Prony serisi çekme. 200°C'de sürünme deney verileri ve Prony serisi çekme.

200°C'de sürünme deney verileri ve Prony serisi çekme şekil 6, ve referans sıcaklık olarak 200 ° C ayar, vardiya faktörleri, 200 ° C ila 120 ° C ve 300 ° ila 200 ° C C, arsa içinde ölçeklenebilir. WLF denklemi vites faktörleri ile değiştirilmesiyle, 200°C'de sürünme deney verileri ve Prony serisi çekme: 200°C'de sürünme deney verileri ve Prony serisi çekme. bu nedenle, kılıf malzemesi P110T için WLF denklemi olan

\log α_{T} = - \frac{45.03 (T - 200)}{4640 + (T - 200)}

(13)

FE simülasyon ve uygulama

FE modeli

numune gerilim sünme testin sayısal simülasyon ticari FE yazılım AbaQus'ü kullanılarak gerçekleştirilmiştir. kılıf malzemesi P110T sürünme deneyi yükleme baz alarak, FE mekanik modeli kurulmuştur, sürünme deney koşullarını gösterir şekil 8. elastik özellikler, elastik modül ve Poisson oranı dahil olmak üzere, 1.99105 Mpa × ve 0.3, sırasıyla, ABAQUS tanımlandığı gibidir. dışında, viskoz özellikleri, gevşeme zamanı ve Prony serisi dahil, 200°C'de sürünme deney verileri ve Prony serisi çekme 3, Ayrıca ABAQUS tanımlandığı gibidir. Dahası, termo-reolojik basit (TRS) parametreler, 200°C'de sürünme deney verileri ve Prony serisi çekme, WLF denklemi ile elde edilen, Ayrıca bu simülasyonda dahildir, ve * analiz visko tipi viskoelastik davranış için uygulanmıştır.

şekil 8. 200°C'de sürünme deney verileri ve Prony serisi çekme.

Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir. şekil 9(bir)-(c), sırasıyla. sıcaklıkta 200 ° C, Simülasyon sonuçları da sürünme deneysel veri ile eşleşen. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir. (13). Ancak sıcaklıklar 120 ° C ile 300 ° C, termo-reolojik davranış, Deneysel ve simüle sonuçlar arasında küçük farklılıklar vardır, ve en büyük fark daha azdır 8%. Bu farkın nedeni, çünkü, FE analizi için, termo-reolojik parametreler simülasyon içine uygulanır, WLF denklemi elde edilir. WLF denklemde, 200 ° C referans sıcaklık olarak alınır, Böylece, içinde şekil 7, Kırmızı eğri mavi eğri ve siyah eğrisinin pozisyonuna kaydırılır. Ve, Yeni kaymış eğriler kılıf malzemenin ısıyla reolojik davranışı temsil eder ve WLF denklemi çözmek için kullanılır. kaymış eğriler Çünkü olmaz 100% Orijinal biriyle de maç, Deneysel sonuçlar elde edildiği, sapma deneysel ve simülasyon arasında var. Ayrıca, 200 ° C bir referans sıcaklık olarak alınır gibi, simülasyon sonucu diğerlerinden daha doğru, sürünme deney koşullarını gösterir şekil 9. bu nedenle, Simülasyon sonuçları bu makalede viskoelastik teori ve TRler yönteminin geçerliliğini göstermek. Ek olarak, FE modeli farklı mekanik ve termal koşullar altında gövde malzemesi P110T viskoelastik davranışı tahmin etmek için de kullanılabilir.

şekil 9. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir.: (bir) 120° C, (b) 200° C, ve (c) 300° C.

sızdırmazlık yüzeyindeki İletişim basıncı

5.5 "SL-APOX ortak bağlantı türü geometrisine göre, sızdırmazlık yüzeyi, eksenel simetri FE modeli ABAQUS inşa edilmiş, sürünme deney koşullarını gösterir şekil 10. İç duvar uygulanan gaz basıncı altında olan. Şekilde kırmızı çizgi sızdırmazlık yüzeyi temsil. Gaz basınç sızdırmazlık yüzeyi ile bir temas basıncı daha yüksek olması halinde, eklem bağlantı sızıntı olasılığı daha yüksektir olacak.

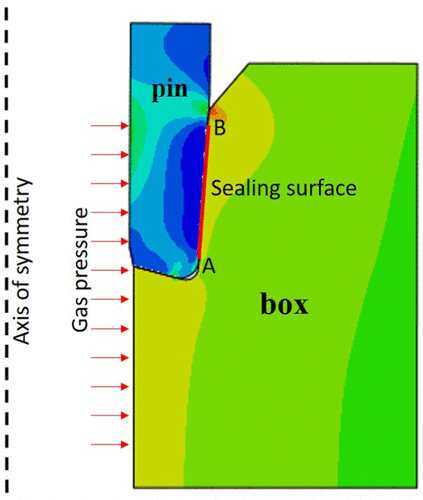
şekil 10. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir..

yüksek sıcaklık ortamında en, sızdırmazlık yüzeyi ile bir temas basıncı nedeniyle malzeme viskoelastisite zamanla azalacaktır. iç duvarına gaz basıncı 75 MPa olarak ayarlanır. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir. şekil 11. Simülasyon sonuçları ilk ortalama temas basıncı 116 ile 160 ° C MPa ile 230 ° C olduğunu göstermektedir. Sonra, Ortalama pres basıncı zamanla azalır. Ortalama temas basıncı 76 MPa'ya damla. Premium bağlantıların kasasını ve gaz sızdırmazlık mekanizmasını gösterir, 230 ° C'de azalan basınç oranı, 160 ° C'lik bir ortamda olandan daha hızlı. 4000 saat içinde olduğu gösterilmiştir (166günler), Temas basıncı 230 ° C 'de 76 MPa düşer. ancak, daha düşük bir sıcaklık ortamında, o 9000 h alacak (375günler) 76 MPa düşmesi.

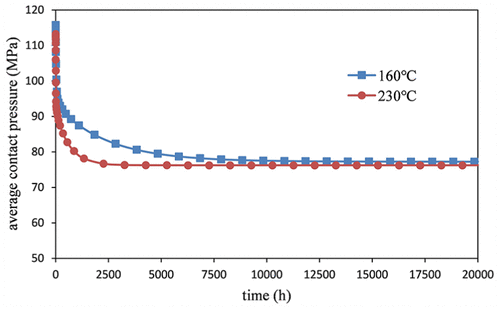
şekil 11. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir..

simülasyon sonucuna göre, ilk temas basıncı oranı ve finial temas basıncıdır 1.56, bu vasıtalar,, yüksek sıcaklık ortamında, sızdırmazlık yüzeyinde son temas basıncı neredeyse üçte bir oranında düşecek. güvenlik faktörü denklem göre

n = \frac{[σ]}{σ_{gp}}

(14)

Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir., $[σ]$ Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir., $σ_{gp}$ Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir.. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir. 2 Emniyet değerlendirilmek üzere.

Sonuç

Premium bağlantısının conta yüzeyi ile bir temas basıncı gevşeme yüksek sıcaklık, doğal gaz kuyusundan de muhafazanın gaz sızıntısı için ana sebebidir.
yüksek sıcaklıklarda, sünme gerilimi deney gövde malzemesi P110T viskoelastik davranışı incelemek için kullanılmıştır. mahfaza malzemenin mekanik davranışının oldukça bağlıdır sıcaklıktır. daha yüksek bir sıcaklık ortamı, Daha hızlı sürünme oranıdır.
kılıf malzemesi P110T için yapısal modeli sürünme deneysel verilerle elde edilmiştir, ve Prony dizi parametre hesaplanmıştır. termo-reolojik davranışı araştırıldı, 300 ° C ve 120 ° C arasında çevre sıcaklıkları arasındaki malzemenin kayması faktörleri elde edilir.
Malzeme P110T için bir viskoelastik FE modeli kurulmuştur, ve simülasyon sonuçları deneysel verilerle iyi uyum.
premium bağlantılı bir sızdırmazlık yüzeyinin FE modeli ABAQUS inşa edildi, ve temas basıncı gevşeme araştırılmıştır. Sızdırmazlık yüzeyindeki tasarımı temas basıncı yüksek sıcaklık doğalgaz kuyularında niyetinde gaz sızdırmazlık basıncı iki katı kadar olması gerektiğini tavsiye edilir.

Taşıma Editör: Michal Kuciej

çatışan çıkarlar Bildirgesi
Yazar(s) Araştırmaya göre herhangi bir çıkar çatışması beyan, yazarlık, Bu maddenin ve / veya yayın.

Referanslar

Teodoriu, C, Kosinowski, C, Amani, M. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir.. Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir. 2013; 2: 1Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir..

Paul Cernocky, E, Valigura, GA, Scholibo, Üç farklı sıcaklıktaki sürünme deney verileri ile simülasyon sonuçları arasındaki karşılaştırma aşağıdaki şekilde gösterilmiştir.. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, işleme toleransları, ve uygulanan yüklere. İçinde: Idelsohn, S, Oñate, E, Dvorkin, E (eds) Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım: Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, 1988, Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım.

Ong, G, Nizam Ramli, M, Ahmad, 'H. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım. İçinde: Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, 22Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım 2016, Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım://Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım

Sugino, M, Yamaguchi, S, Ugai, S., yenilikçi, yüksek performanslı prim için bağlantı dişli BAKINIZ. Nippon Steel & Sumitomo Metal teknik rapor yok. 107, Şubat 2015, Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, http://Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım

Takano, J, Yamaguchi, M, Kunishige, 'H. yüksek sıkıştırma dayanabilecek için prim bağlantısı Gelişimi “KSBEAR”, Yüksek dış baskı, ve bükme sever. Kawasaki Steel teknik rapor yok. 47, 2002, http://Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım

Kim, J, rüzgâraltı, HS, Kim, n. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım 2010; 136: 1067Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım. 3

Lopes, J, Alberto, C, Tomas, J. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım. Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım 2015; 12: 420Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım.

Tasarım geometrisinin bir fonksiyonu olarak nispi sızdırmazlık performansı oluşturmak için muhafaza-boru bağlantılarının sonlu eleman analizine standart bir yaklaşım, GB, Schapery, RA. Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri. Prony serisi göre Bölüm I-sayısal bir yöntem. Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri 1999; 26: 1653Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri.

Ananthsynm, B. Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri. Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri 326, 2008, http://Doğrusal viskoelastik malzeme fonksiyonları arasında dönüşüm yöntemleri